Some Important Concepts For BECC-105 TEE Prep

Utility Functions and Risk Attitudes

• Risk-neutral consumer: Utility function is linear in wealth, e.g., U(W) = a + bW (b > 0). The graph is a straight upward-sloping line. Marginal utility of wealth is constant. Expected utility of a gamble equals utility of expected wealth: EU(gamble) = U(E[W]). Indifferent to fair bets or fair insurance.
• Risk-averse consumer: Utility function is strictly concave in wealth, e.g., U(W) = √W or U(W) = –e^(–αW) (α > 0). The graph bends downward (diminishing marginal utility). Jensen’s inequality gives U(E[W]) > EU(gamble). Prefers certain outcome over risky gamble with same expected value.
• Risk-taking (risk-loving) consumer: Utility function is strictly convex in wealth, e.g., U(W) = W² (for W > 0). The graph bends upward (increasing marginal utility). U(E[W]) < EU(gamble). Prefers gamble over certain outcome.

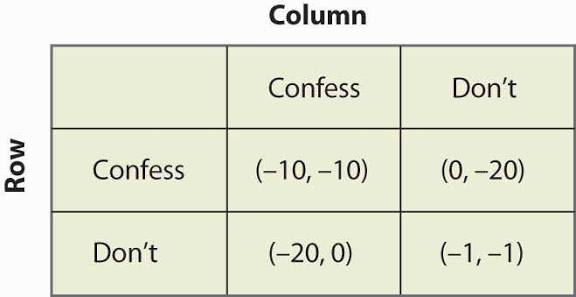
Who buys insurance?

Only the risk-averse consumer buys insurance (even at a slightly unfair premium, i.e., premium > expected loss). Insurance converts a risky prospect into a certain one, raising expected utility. Risk-neutral is indifferent at fair premium and refuses unfair. Risk-loving refuses insurance and may even buy lottery tickets.

Slutsky’s Substitution Effect

Slutsky decomposition splits the total price effect (Δx/Δp) into:

1. Substitution effect (Slutsky): change in demand when relative prices change but real income (purchasing power) is held constant by compensating income so the consumer can just afford the original bundle (stays on the original indifference curve).
2. Income effect: the remaining change due to the effective change in real income.

Graphically (for a price fall of X):

• Original equilibrium: point A (budget line BL₁ tangent to IC₁).
• New price: steeper pivot to BL₂, new equilibrium C on higher IC₂.
• Draw a compensated budget line BL′ parallel to BL₂ but tangent to original IC₁ at point B.
• Movement A → B = pure Slutsky substitution effect (always negative for own-price).
• Movement B → C = income effect.

Sara’s Equilibrium Consumption Bundle (Lagrangian)

Given: U(X, Y) = X^{0.25} Y^{0.75}, P_X = ₹5, P_Y = ₹3, M = ₹400.Lagrangian:
L = X^{0.25} Y^{0.75} + λ (400 – 5X – 3Y)First-order conditions:
∂L/∂X = 0.25 X^{-0.75} Y^{0.75} – 5λ = 0
∂L/∂Y = 0.75 X^{0.25} Y^{-0.25} – 3λ = 0
∂L/∂λ = 400 – 5X – 3Y = 0From first two: MRS = P_X / P_Y
(0.25/0.75)(Y/X) = 5/3
(1/3)(Y/X) = 5/3
Y/X = 5 ⇒ Y = 5XPlug into budget:
5X + 3(5X) = 400
20X = 400
X* = 20, Y* = 100

Walras’ Law

In a general equilibrium model, the total value of excess demands is zero:
Σ p_i z_i(p) ≡ 0
(where z_i = excess demand for good i).
It follows from budget constraints: if all agents spend exactly their income, the value of what is demanded extra must equal the value of what is supplied extra. One market’s excess demand implies offsetting excess supply elsewhere.

Isoquant and Economic Region of Production

An isoquant is the locus of all combinations of two inputs (L, K) that produce a given level of output Q₀: Q = f(L, K) = constant.

Ridge lines are the loci where marginal product of one input becomes zero:

• Upper ridge line: MP_L = 0 (isoquants become vertical).
• Lower ridge line: MP_K = 0 (isoquants become horizontal).

The economic region of production lies between the two ridge lines because:

• Inside: both MP_L > 0 and MP_K > 0 → rational input use (positive marginal contributions).
• Outside: one MP ≤ 0 → firm would never operate there (adding the input reduces or does not increase output).

https://artifacts.grokusercontent.com/third-party-image

Economic Profit of a Competitive Firm

Economic profit = Total Revenue – Total Economic Cost
= TR – (Explicit costs + Implicit/opportunity costs)
In perfect competition, long-run economic profit = 0 (normal profit only).

Long-Run Equilibrium of a Perfectly Competitive Firm

• Market: free entry/exit until P = min LRAC.
• Firm: produces where P = MR = MC = min LRAC (at efficient scale).
• Zero economic profit → no entry or exit incentive.
• Productive and allocative efficiency.

https://artifacts.grokusercontent.com/third-party-image

Optimal Consumption Bundle: Quantity Tax vs Equivalent Income (Lump-Sum) Tax (Indifference Curve Analysis)

Assume a tax on good X. Quantity (specific) tax t per unit on X:

• Budget line pivots inward (steeper slope: new P_X = old P_X + t).
• New tangency on lower indifference curve → substitution + income effect. Bundle has less X, more Y (if normal).

Equivalent lump-sum (income) tax:

• Same government revenue collected, but income reduced by fixed amount T = t × X₁ (where X₁ is pre-tax quantity).
• Budget line shifts parallel inward.
• New tangency usually allows more X than under quantity tax (only income effect, no substitution effect away from X).
• Quantity tax distorts relative prices more; lump-sum is non-distortionary (for revenue raising).

Explain any two

(i) Quasi-linear preferences

U(x, y) = x + v(y) (or v(x) + y).

• Marginal utility of one good (usually y) is constant → income effect is zero for the other good (x).
• All income effects fall on y (“money”).
• Demand for x depends only on its price, independent of income → no income effect on x. Useful for welfare analysis (consumer surplus = area under Marshallian demand) and partial equilibrium.

(iv) First Fundamental Theorem of Welfare Economics

Any competitive (Walrasian) equilibrium allocation is Pareto efficient (no one can be made better off without making someone worse off), provided:

• Local non-satiation,
• Perfect competition,
• No externalities,
• Complete markets.
  It says “the invisible hand” works: self-interested market behaviour leads to socially efficient outcome.

Distinguish any two

(i) Returns to scale vs Law of Variable Proportions

• Returns to scale: long-run concept; all inputs increased proportionately → output response (increasing/constant/decreasing). Describes production function homogeneity.
• Law of Variable Proportions (diminishing returns): short-run; one input varied, others fixed → three stages (increasing, diminishing, negative returns). Caused by fixed factor.

(iii) Cardinal vs Ordinal analysis

• Cardinal: utility measurable in absolute units (e.g., 10 utils, 20 utils). Allows interpersonal comparison, marginal utility, etc. (old Marshallian).
• Ordinal: utility only ranked (IC₁ > IC₂). No magnitude or interpersonal comparison. Modern Hicksian/Arrow-Debreu approach; sufficient for demand theory.

This covers the entire question set with rigorous step-by-step explanations and standard diagrams referenced visually where required.